【数据结构】直接插入排序

news/发布时间2024/7/27 12:11:15

大家好，我是苏貝，本篇博客带大家了解插入排序，如果你觉得我写的还不错的话，可以给我一个赞👍吗，感谢❤️

一. 基本思想

直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
实际中我们玩扑克牌时，就用了插入排序的思想

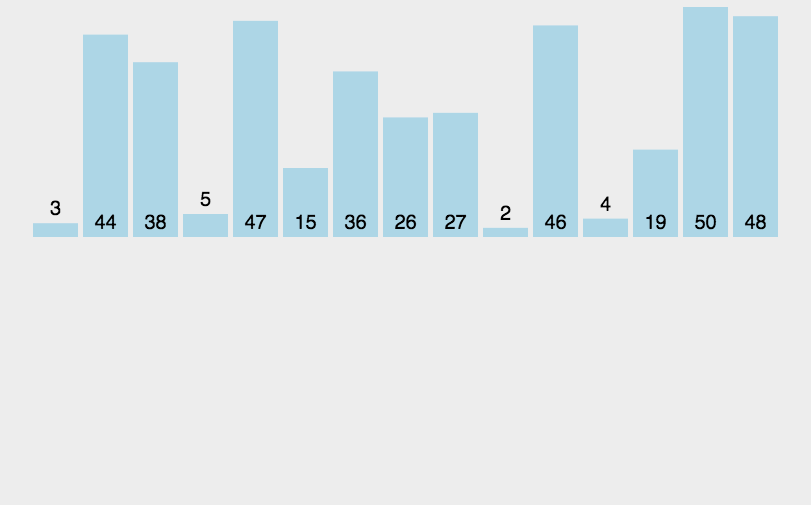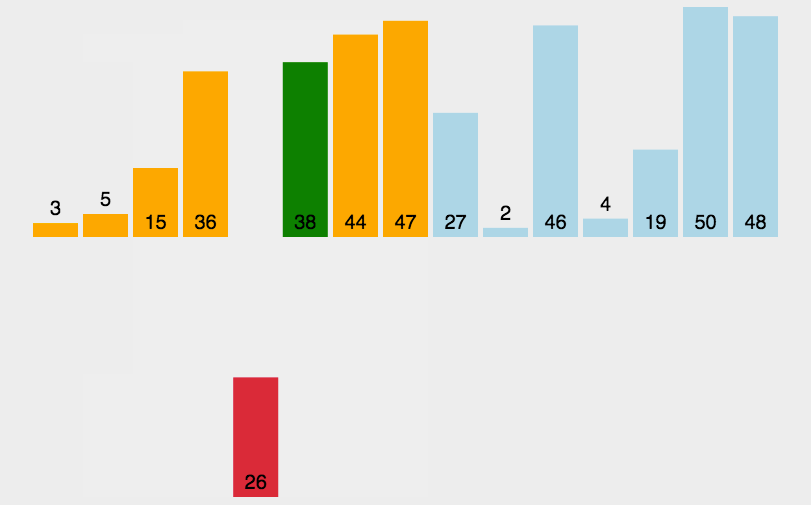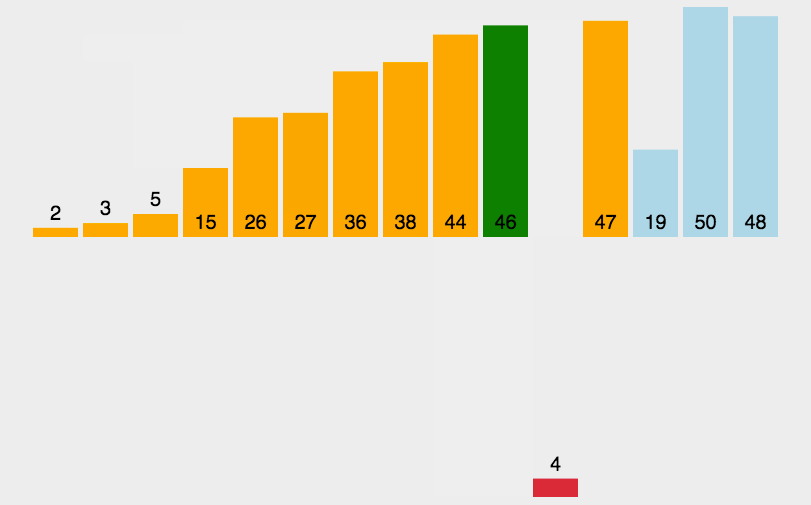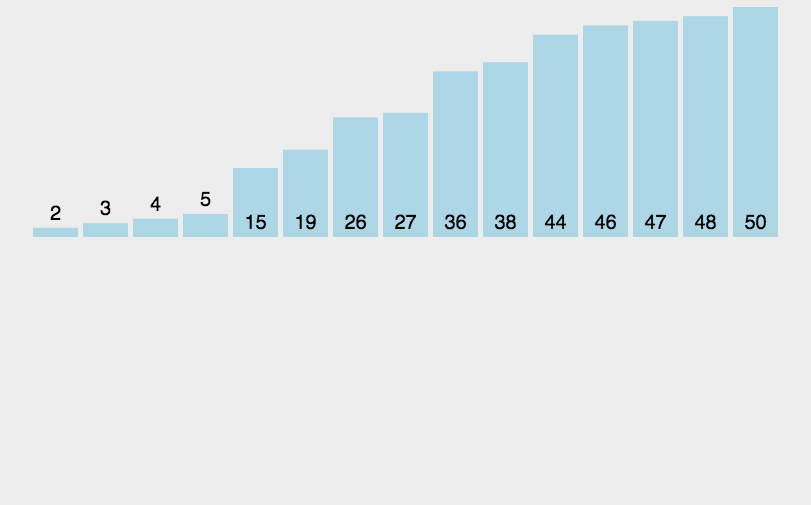
在这里插入图片描述

二. 插入排序详解（以升序为例）

思路：

我们让数组下标为[0,end]的有序，现插入a[end+1]，使数组下标为[0,end+1]的有序。
最开始时，我们让end==0，这样就是插入a[1]，让数组下标为[0,1]的有序

在这里插入图片描述

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移

下面代码中，因为最后一个元素一定是tmp，所以end+1<n，所以end<n-1，因为end=i，所以i<n-1。

void InsertSort(int* a, int n)
{//假设[0,end]有序，将a[end+1]插入再次形成有序for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tmp;}
}

插入排序的时间复杂度是多少？
时间复杂度是在最坏情况下计算的，插入排序的最坏情况就是降序
第一次：1
第二次：2
……
第N-1次：N-1
全部加起来=1+2+……+(N-1) = (N+1)(1+N-1)/2 = N*(N-1)/2，所以时间复杂度为O(N^2)

直接插入排序的特性总结：
1.元素集合越接近有序，直接插入排序算法的时间效率越高
2.时间复杂度：O(N^2)
3.空间复杂度：O(1)，它是一种稳定的排序算法
4.稳定性：稳定

三. 对比冒泡排序

点击了解冒泡排序

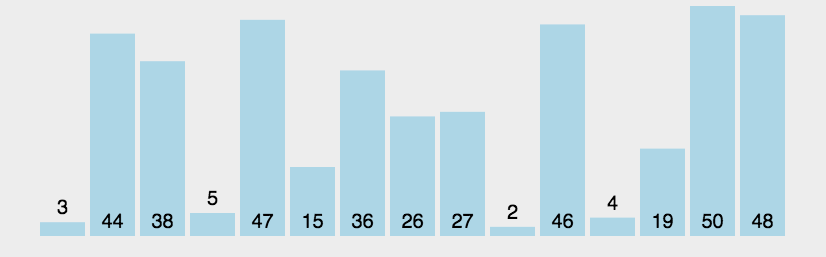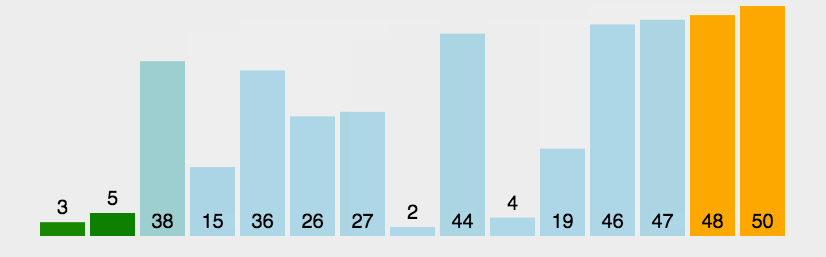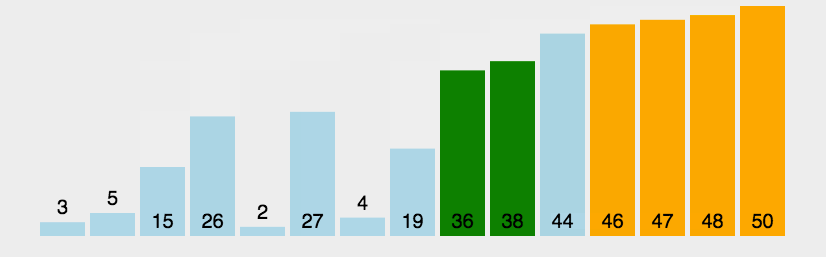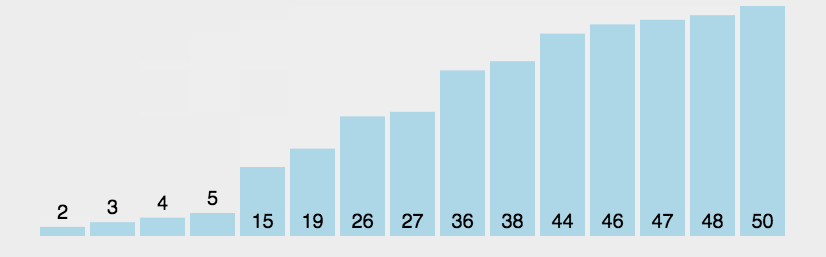
在这里插入图片描述

void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}

冒泡排序的时间复杂度是多少？
总共需要冒泡N-1次
第一次冒泡：循环N-1次
第二次冒泡：N-2
第三次冒泡：N-3
…
第N-1次冒泡：1
全部加起来=1+2+……+(N-1) = (N+1)(1+N-1)/2 = N*(N-1)/2，所以时间复杂度为O(N^2)

所以插入排序和冒泡排序的时间复杂度是一样的，那能说明它们的效率是一样的吗？在这里我们用一个函数来测试两个排序的性能。让两种排序都排列同样的100000个随机数字，比较2个排序的时间。rand函数用来生成随机值，clock函数用来返回程序运行的时间。因为2种排序用的时间都比较长，所以在这里我们将Debug换成Release

void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();BubbleSort(a7, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("BubbleSort:%d\n", end2 - begin2);free(a1);free(a2);
}